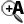Dans cet article je vais assembler des éléments publiés sur twitter avec des schémas perso et tout un tas d’autres trucs que je trouverai pour exposer ce qui n’est pour l’instant qu’une intuition vu que je manque de connaissances solides en physique mais qui peut se résumer à ceci : la dialectique est étriquée, un changement de regard sur le monde le révèle bien plus complexe et ... fractal.

Comme pour le reste de mes "recherches" de non spécialiste, si je partage du contenu cela ne vous autorise pas à le PILLER mais je suis ouvert à l’échange ici : frisevial@librairiemobile.org ou là lumomana@riseup.net

david vial

mais yeps !
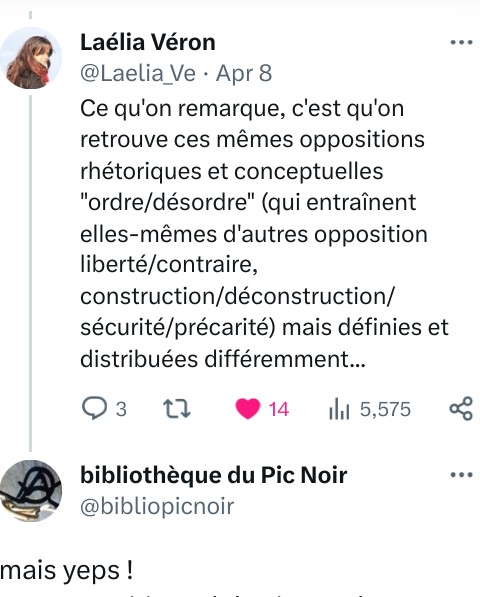
Des oppositions rhétoriques dans lesquelles on peut retrouver d’autres oppositions rhétoriques (qui même peuvent s’inverser) ... C’est comme dans une structure fractale : et peut-être que par là on peut échapper à une dialectique trop etriquée

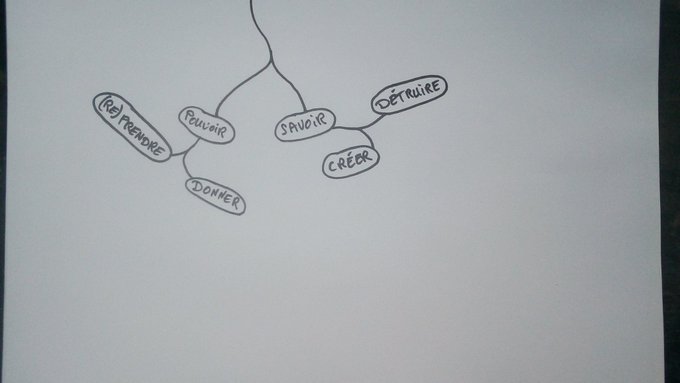
si on ajoute recevoir, on a par exple,
. recevoir (de la visite) =
. accueillir (unE compa)
ou . subir (une perquiz)

. donner (la main) =
. imposer (une direction (souvent pr traverser la rue 🙃)
ou . offrir (une aide)

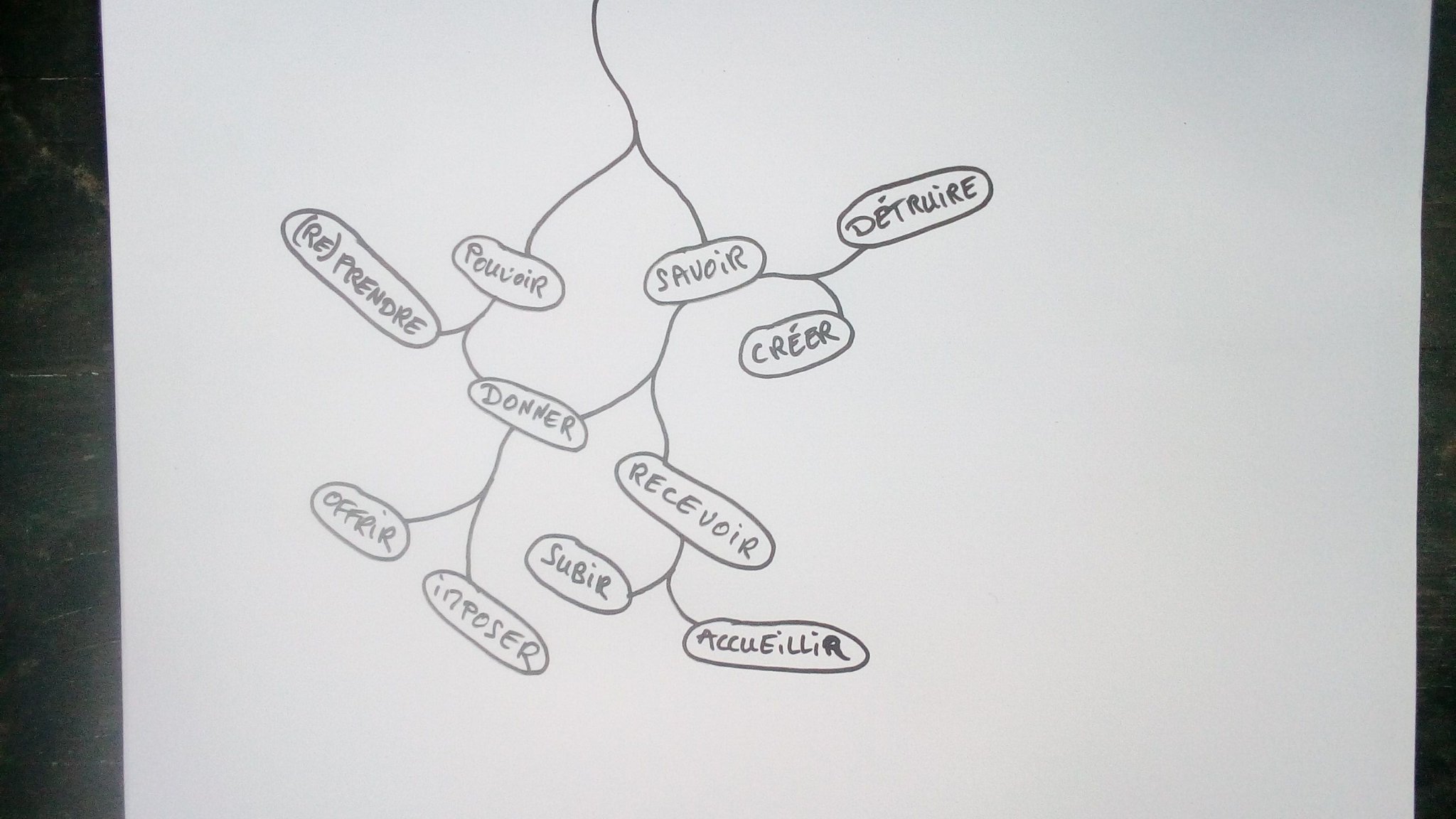
Ça n’a l’air de rien comme ça
Pourtant, me semble que
passer de
.................... recevoir/ donner
à accueillir / subir / imposer / offrir

ajoute un niveau de compréhension
(mais compris par qui ?)

  - - - - -

Ah voilà ! ⬇️
je savais bien que la dialectique peut devenir fractale si on s’en affranchi pour changer de point de vue

(mais alors où cela mène-t-il ?)

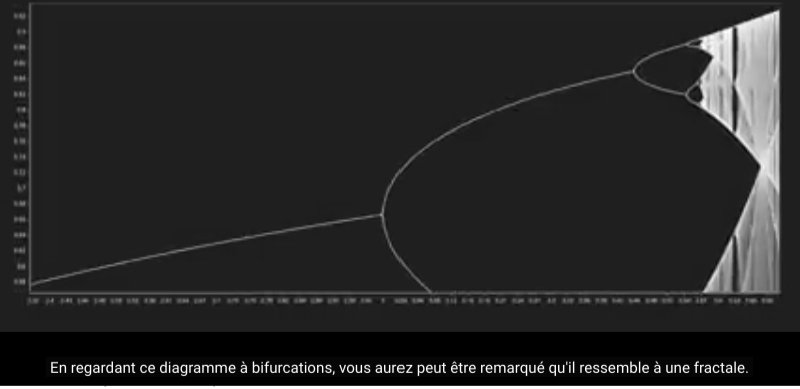
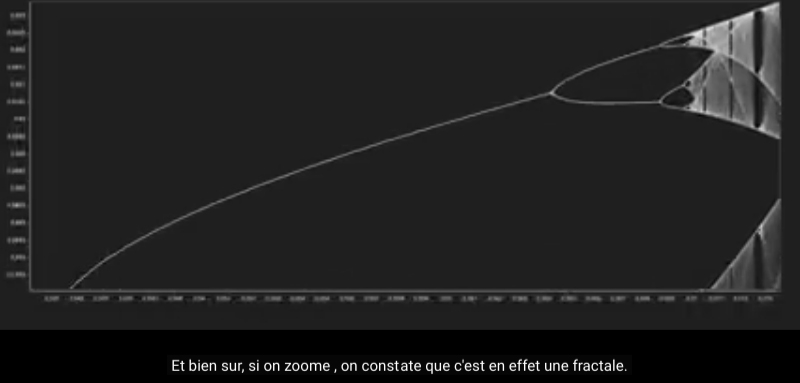
Source des graphiques : https://m.youtube.com/watch?v=ovJcsL7vyrk

si on regarde le monde de biais, il semble fait d’oppositions symétriques (noir/blanc mâle/femelle nuit/jour ...)
alors que si on le regarde en face, il apparaît plutôt fractal

je vous laisse penser à tout ça tranquillement..

https://m.youtube.com/watch?v=O-hOWNjFh2M&list=PLm-qHtxVDg42bzjyEK-K1KqN-Cofo-Sb5&index=19

A propos de cette correspondance entre bifurcations et fractale et comment on peut les distinguer en changeant de point de vue

https://www.researchgate.net/figure/Correspondence-between-the-Mandelbrot-set-a-and-the-Feigenbaum-bifurcation-tree-b_fig2_228635212

pour illustrer cette idée pas si farfelue me semble t-il, d’un univers multiple dont la structure fractale épouse en profondeur les contours de la complexité de nos imaginaires, on peut voir ce film d’animation : " le tableau"

https://m.youtube.com/watch?v=pUTV6gF-5pQ

Car vous doutez que l’univers soit fractal ? N’est ce pas ?

Pourtant, cette "fractalitude" a déjà surgit dans l’environnement...
Si si !
Avec l’
"Anamorphic flloor art"

https://www.pinterest.fr/pin/761600987005246099/

https://www.pinterest.fr/pin/508625351661834944/

La page linktr.ee/librairiemobile est (peut-être) une expérience pour mettre en évidence cette hypothèse ? un objet singulier dans lequel on peut "zoomer" ou plonger pour découvrir d’autres univers singuliers, eux mêmes composés d’assemblages etc ..

ne pas s’arrêter au titre... cette vidéo explique des trucs intéressants⬇

Les notions abordées dans cet article ⬇️ sont tout à fait novatrices mais aussi complexes...
j’ai demandé un résumé en langage courant à manus.im que je mets ci-dessous.

A propos de cette correspondance entre bifurcations et fractale et comment on peut les distinguer en changeant de point de vue
https://www.researchgate.net/figure/Correspondence-between-the-Mandelbrot-set-a-and-the-Feigenbaum-bifurcation-tree-b_fig2_228635212

# Résumé explicatif : Généralisation complexe de l’analyse de groupe de renormalisation et ensemble de Mandelbrot - Une analogie thermodynamique

Ce document scientifique explore les liens fascinants entre les mathématiques des systèmes dynamiques complexes et la physique des transitions de phase. Voici une explication en langage courant des concepts principaux.

## Qu’est-ce que l’analyse de groupe de renormalisation ?

L’analyse de groupe de renormalisation (RG) est une méthode mathématique développée par Feigenbaum en 1978 pour étudier comment les systèmes évoluent lorsqu’on change d’échelle d’observation. Imaginez que vous observiez un flocon de neige : en zoomant sur une partie, vous retrouvez des motifs similaires à l’ensemble. Cette propriété d’auto-similarité est au cœur de l’analyse RG.

Dans ce document, les chercheurs étudient une équation mathématique simple mais riche en comportements : x_n+1 = λ - x_n². Cette équation décrit comment une valeur évolue dans le temps en fonction d’un paramètre λ. Selon la valeur de ce paramètre, le système peut avoir un comportement stable, périodique ou chaotique.

## L’ensemble de Mandelbrot : une carte du chaos

L’ensemble de Mandelbrot est probablement l’une des figures mathématiques les plus célèbres. Il s’agit d’une sorte de "carte" qui montre, pour chaque valeur du paramètre λ (considéré comme un nombre complexe avec une partie réelle et une partie imaginaire), si le système reste stable ou s’échappe vers l’infini.

Visuellement, l’ensemble de Mandelbrot ressemble à un bonhomme de pain d’épice avec une grande forme en cœur (appelée cardioïde) entourée de cercles et de structures fractales complexes. Chaque point de cette carte représente un comportement différent du système :
 Les zones grises correspondent à des comportements périodiques (le système répète les mêmes valeurs)
 Les zones noires correspondent à des comportements chaotiques mais bornés
 Les zones blanches correspondent à des comportements qui s’échappent vers l’infini

## L’ensemble de Julia : frontière entre ordre et chaos

Pour chaque valeur du paramètre λ, on peut définir un autre ensemble appelé "ensemble de Julia". Cet ensemble représente la frontière entre les points qui restent stables et ceux qui s’échappent vers l’infini lorsqu’on applique répétitivement notre équation.

L’ensemble de Julia peut être vu comme une frontière de phase, similaire à la frontière entre l’eau et la glace lors d’un changement d’état. Cette frontière a une structure fractale, c’est-à-dire qu’elle présente des motifs qui se répètent à différentes échelles.

## L’analogie avec la thermodynamique

La contribution majeure de ce document est d’établir une analogie entre ces concepts mathématiques et la théorie des transitions de phase en physique :

1. **Les transitions de phase** : En physique, une transition de phase se produit lorsqu’un système change d’état (comme l’eau qui se transforme en glace). Ces transitions sont caractérisées par des changements brusques dans les propriétés du système.

2. **La théorie de Yang-Lee** : Cette théorie décrit les transitions de phase en termes de "zéros" d’une fonction mathématique appelée "fonction de partition". Les chercheurs montrent que ces zéros correspondent aux points de l’ensemble de Julia.

3. **La limite thermodynamique** : En physique, on considère souvent la limite où le nombre de particules tend vers l’infini. Les auteurs montrent que cela correspond à la limite où la période des cycles dans le système dynamique tend vers l’infini.

## Une nouvelle façon de comprendre le chaos

Les auteurs proposent une analogie électrostatique pour mieux comprendre la transition vers le chaos. Ils montrent qu’on peut définir un "potentiel électrostatique" associé à l’ensemble de Julia, qui se comporte comme un paramètre d’ordre pour la transition vers le chaos.

Au point de transition, ce potentiel présente un saut dans sa dérivée, similaire au saut d’énergie libre lors d’une transition de phase de type II en thermodynamique. Cette observation permet de définir un nouveau critère mathématique pour identifier précisément le seuil entre comportement ordonné et chaotique.

## Pourquoi est-ce important ?

Cette recherche établit des ponts entre différents domaines des mathématiques et de la physique. En montrant que les systèmes dynamiques complexes peuvent être analysés avec des outils similaires à ceux utilisés pour les transitions de phase, les auteurs ouvrent de nouvelles perspectives pour comprendre les phénomènes critiques et le chaos.

Ces analogies permettent de transférer l’intuition et les méthodes d’un domaine à l’autre, enrichissant notre compréhension des systèmes complexes en général. Elles suggèrent également que les transitions vers le chaos pourraient être étudiées de manière plus systématique en utilisant les concepts de la thermodynamique.

En conclusion, ce document propose une généralisation élégante de l’analyse de groupe de renormalisation aux systèmes dynamiques complexes, établissant des parallèles profonds avec la physique des transitions de phase et offrant de nouvelles perspectives pour l’étude des phénomènes critiques à la frontière entre ordre et chaos.